如何平冠状病毒的曲线,一个数学家解释

人到澳大利亚旅行现在必须self-isolate 14天周末宣布一系列措施由首相斯科特•莫里森,目的是减缓冠状病毒的传播和宽松医院病床上的压力。
减缓病毒的传播的一般概念被称为“平曲线”epidemiologists-experts研究疾病发生频率在不同的人口,以及为什么。这个词已经成为广泛的社交媒体上的为鼓励公众实践“社会距离”。
但社会距离如何帮助平曲线?我们可以通过指解释数学家称之为“指数增长”。
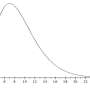
指数级增长
在流行病的早期阶段,当大多数人都容易受到感染,数学家模型可以在人与人之间传播的疾病基本上是一个随机的“分支过程”。
如果感染者感染其他两个平均感染者双打每一代的数量。这个组合被称为指数级增长。
当然,受感染的人不是肯定去感染别人。有许多因素影响感染的可能性。在大流行,增长率取决于平均一个人可以感染的人数,和时间这些人成为感染自己。
研究表明确诊COVID-19病例的数量呈指数级增长全球数量翻了一番大约每六天
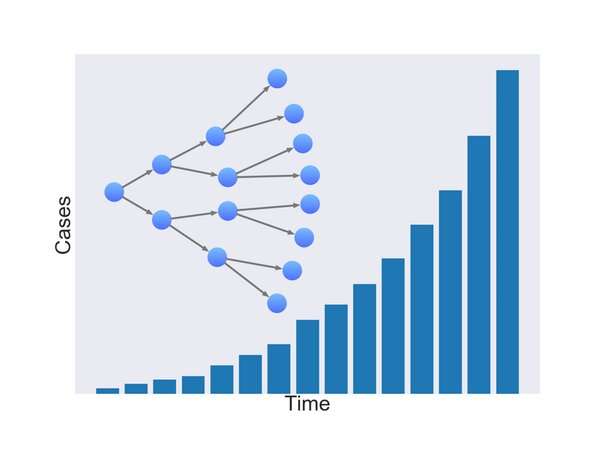
指数增长模型匹配现实从少数感染者在人口多,如病毒在武汉第一次出现时,或当它来到意大利或伊朗。
但这不是一个好的模型一次大量的人被感染。这是因为感染者接触一个敏感的人的机会下降,因为有更少的易感人群,越来越多的人恢复和发展一定程度的免疫力。
最终,感染者的机会接触一个敏感的人变得足够低的感染率降低,导致更少的情况下,最终,结束的病毒传播。
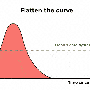
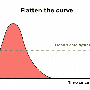
平曲线
世界各地的卫生当局已无法完全防止COVID-19的传播。如果情况下双每六天,然后医院,尤其是重症监护病房(icu),会很快被淹没,让病人没有必要的护理。
但是,增长速度可以通过减少放缓的平均数量情况下单一的情况产生。
在这一过程中,相同数量的人可能会感染,和流行,它们的寿命会更长,但严重病例的数量将会展开。这意味着,如果你画一个图的情况下,随着时间的推移,上升和下降曲线较长但峰值低。“平曲线”这样,icu将不太可能失去能力。
目前还没有疫苗或COVID-19特定的药物,我们可以减少传播的唯一方法是通过良好的卫生习惯,隔离疑似病例,通过社会距离等措施取消大事件和关闭学校。
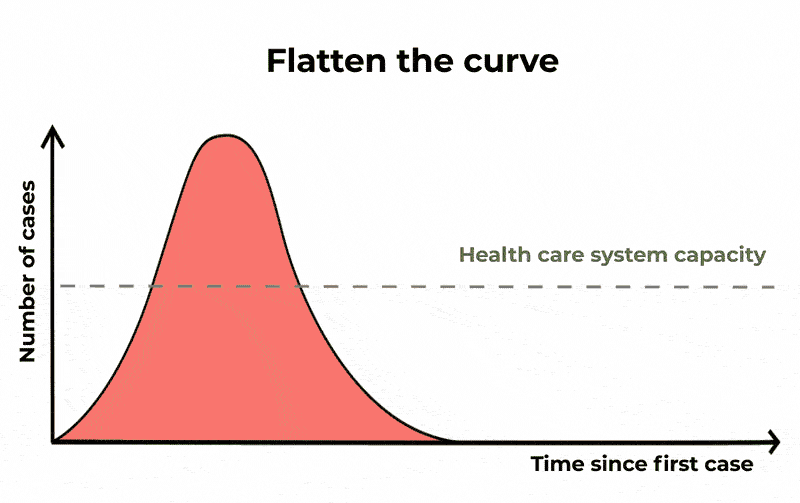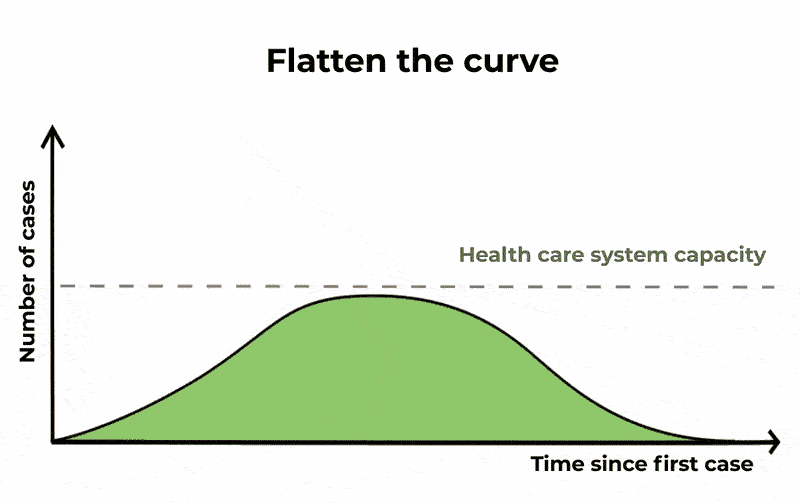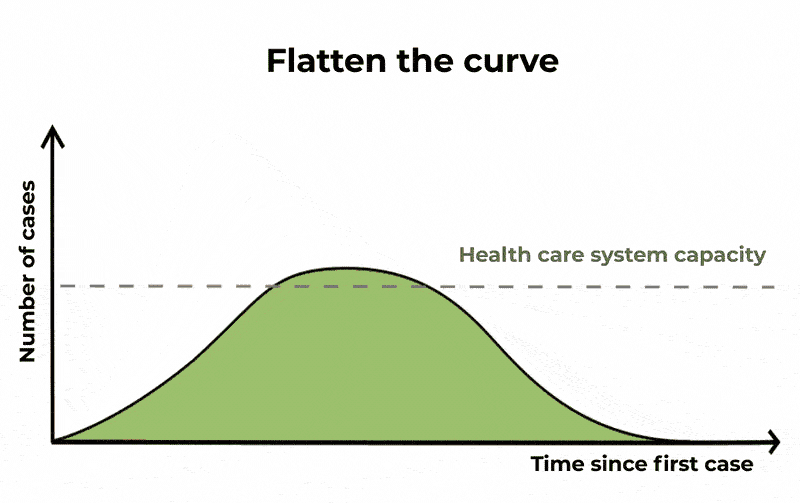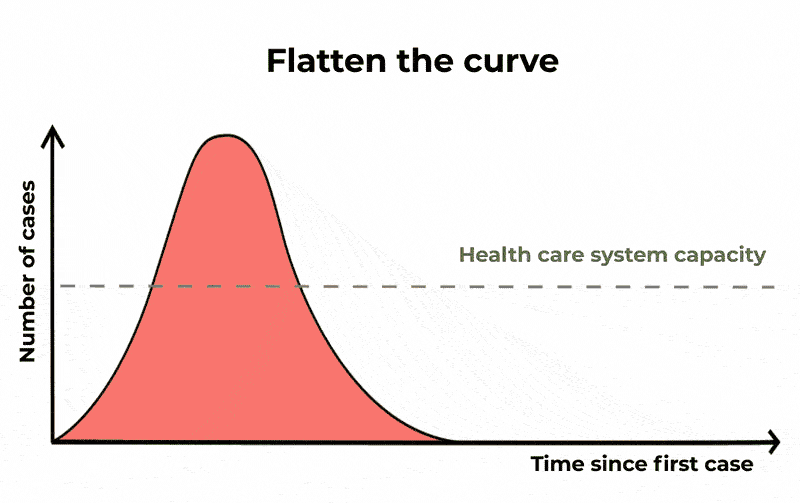
避免“超级传播者”
当然,情况并不是那么简单的作为一个简单的分支过程。有些人比其他人更交互,可能会接触到很多不同的团体。
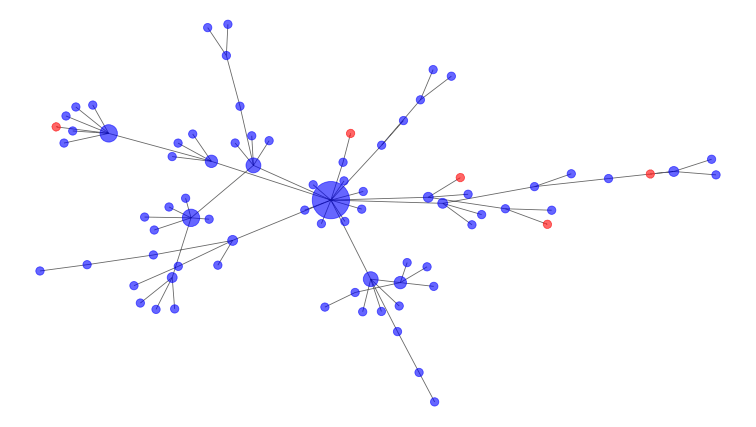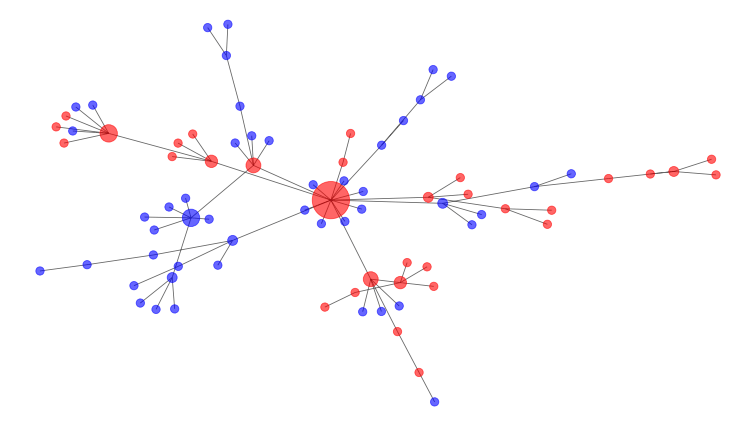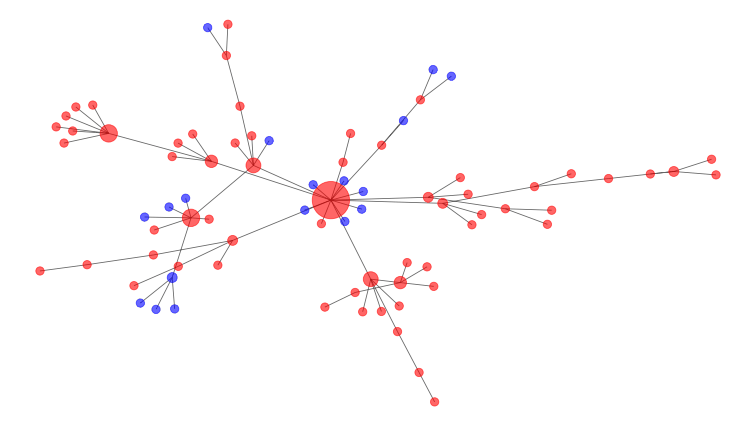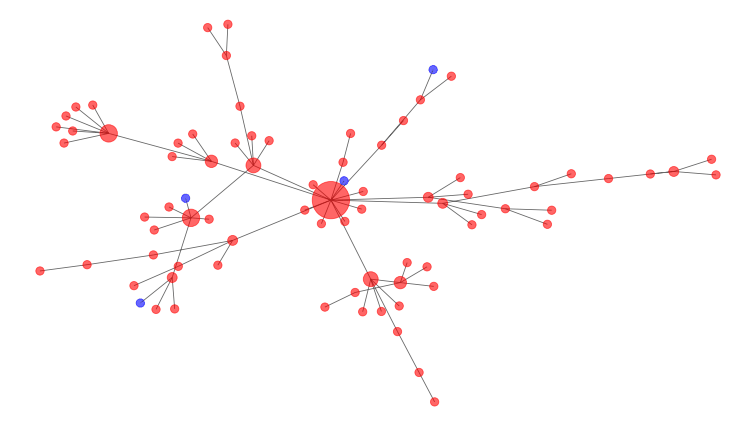
数学家模型这些连接作为一个社交网络,如下面一个。感染者是红色节点和易感人群是蓝色的。中间的大节点的图是一个super-spreader,与许多其他的人,因此更有可能传播疾病。
干预措施帮助删除节点和连接。
在上面的图中,大型、高连接中央节点将是最好的一个打破连接删除。这就是为什么它是一个好主意,以避免大型公共集会期间COVID-19暴发。
社会距离的数学模拟表明打破网络分开可以让感染的曲线变平。
数学是如何帮助
需要多少社会距离平曲线足以防止医院不知所措吗?它足以隔离人接触确诊病例?我们需要广泛的关闭事件,学校和工作场所?
这些问题的答案需要数学建模。
我们仍然处于早期阶段的COVID-19爆发,存在极大的不确定性这种病毒的特点。准确预测COVID-19的增长,底层传输动力学需要确定。
这些驱动因素包括:
- 有多少人平均个体感染吗?(“繁殖数量”,根据世界卫生组织,目前在1.4 - -2.5之间的人)
- 直到出现症状多久?(“潜伏期”,估计5.1天)
- 什么比例的传播发生在出现症状之前,如果有的话?
因此数据被收集并集成到模型在未来的几个月,我们将更好地提供准确的预测COVID-19的进程。
在那之前,最好是宁可谨慎和迅速采取行动来减缓传播,而不是风险激增的情况下,把我们的卫生系统。
进一步探索










用户评论