数学逻辑可以帮助您为冠状病毒测试更多人

在大流行期间,对患者的快速测试具有重要意义。但在那里的时候COVID-19检测不够或测试一直很慢,有没有办法提升这个过程?作为一个数学家和工程师,我问自己,如果有一个理论家可以做些什么来帮助满足世界卫生组织的需求尽可能多地测试患者。
也许有个办法可以测试许多耐心用几个试管。而不是使用一个试管为某人产生一个结果样本,我们可以用几个试管测试更多的样品-在逻辑的帮助下。
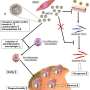
一般想法很简单。从我们每个理论患者采取的样本分布到我们具有不同组合的试管的一半。例如,如果我们有十个试管,我们会将每个患者分配到其中五种的不同组合。
任何测试负面的管子都告诉我们,所有患者都有所分享的患者必须是负的。同时,测试阳性的试管可以含有来自许多阳性患者的样品 - 只有当所有相关的试管都是阳性时,单个患者才能测试阳性。
这种方法特别是在疫情的早期阶段有效,当时可能会测试正面的人。
修改的方法
然而,随着更多患者被感染,鉴定谁具有患者更具挑战性,因为阳性测试的管更可能包括甚至更大的患者组合。为了克服这种困难,必须如下例所示修改该方法。
假设我们有6根试管和20个病人。试管的编号为#1、#2、#3、#4、#5和#6。每个病人都有一个由0和1组成的六位数(二进制系统)。每个数字对应一个试管——“0”表示我们不将样本添加到相应的试管中,而“1”表示我们添加了。

例如,患者#1给出了数字[0 0 0 11 1],这意味着仅测试管#4,#5和#6将包含来自患者#1的样本。患者#2给出了数字[0 0 1 0 11 1],这意味着只有测试管#3,#5和#6将包含来自患者#2的样本。等等,所有20名患者。
在加入所有20名患者的样本后,这6支试管将进行测试。然后,如果测试返回阳性管# 4,# 5和# 6,例如,我们可以说唯一的病人# 1-allocated数量(0 0 0 1 1 1)——将是积极的,因为只有病人样本添加到所有三个试管- # 4,# 5和# 6和没有休息。
现在是困难的部分。假设3号、4号、5号和6号试管的结果是阳性的。我们可以说,所有加入1号和2号试管的患者的样本都是阴性的,但我们不能确定其他的,因为3号、4号、5号和6号试管有多种可能性。是病人[0 0 1 0 1 1]和[0 0 1 1 1 1]生病了,还是可能是[0 0 0 1 1 1],[0 0 1 0 1 1]和[0 0 1 1 1],或者可能都是?所有这些组合将导致试管#3、#4、#5和#6返回阳性。那么,有没有办法确切地知道谁是病人呢?
是的,但前提是现在的检测结果不仅是阳性或阴性,而且还能有一定程度的“阳性”,例如通过识别样本中的抗体量。利用这个,我们可以比较试管之间的“阳性”量,这给我们提供了一个线索,以确定测试阳性的患者的正确组合。
一定程度的“积极性”
回到我们的例子,如果测试管#4和#5中的阳性相同(让我们在两者中说出相同量的抗体),但在#3和#6中不同,我们可以得出结论,患者[0 00 11 1 1]和[0 0 1 0 11]由于来自第一患者的样品[0 0 0 11 1]是管#4和#5的样品,而来自阳性其他患者[0 0 1 0 1 1]在管#5中(但不是#4)。这意味着如果两名患者生病(管#5将具有两种患者的阳性,那么这些试管中的阳性不能是相同的,但管子#4将具有一体的正力)。
患者在管#4和#5中返回相同的阳性的唯一患者是患者[0 0 0 11 1]和[0 0 11 1 0],因为这些来自这些的样品都将添加到两根管中#4和#5,导致两个试管中的阳性相同。
在上面的例子中,我们能够测试20名患者,六个试管少量。但是该方法可以扩大起来,以测试数千名有数千名患者的试管。即使使用机器正在开发的机器可以在五分钟内处理测试,这种方法仍然可以在资源较少的地方更快,更便宜。
然后,我们可以增强收集的样本的测试,特别是在何处,测试是挑战的。在这些情况下,可能有助于减轻新型冠状病毒,拯救许多生命。












用户评论