公共卫生工具预测大流行的影响和缓解努力

流行病学家和公共卫生官员有了一种新的预测工具来分析流行病的过程,这要归功于阿拉巴马大学亨茨维尔分校(UAH)的一位教授与该校校友合作推导出的数学公式。
在期刊审稿人称为开创性的工作中,他们提供了一个数学方法一个描述化学自催化的模型。基于他们在自催化作用和流行病学之间的类比,他们的公式也准确地预测了未来流行病的传播。
研究人员说,这个公式易于评估,可用于判断旨在遏制疫情的各种缓解措施的效果。因此,他们说,它可以帮助公共卫生当局努力部署资源来减轻大流行的影响。
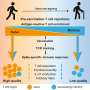
由阿拉巴马大学系统的一部分UAH的化学教授James Baird博士和位于佛罗里达州特伦顿的Alderman Barlow实验室的Douglas a. Barlow博士创建。,该公式计算了病毒或细菌源性疾病的传播,并考虑了各种缓解措施的影响,如口罩、社交距离、隔离、疫苗接种率以及医疗效果。
当催化剂分子与反应物分子结合产生更多的催化剂分子时,化学转化是自催化的,这一结果有助于加速反应。
“在这个意义上,自催化反应完全类似于传染病的传播,”贝尔德博士说。“在疾病病例中,易感者与感染者之间的接触导致两个感染者。”
据贝尔德博士说,他和巴洛博士推导出的公式是1927年英国科学家w·o·克马克(W. O. Kermack)和a·g·麦肯德里克(a . G. McKendrick)提出的流行病数学理论的一个高度精确的近似解,他们的结果发表在《美国科学》杂志上英国皇家学会学报.凯马克是一位生物化学家,麦肯德里克是一名英国军医,他的数学直觉可以与许多专业人士相媲美。
贝尔德博士说:“科马克和麦肯德里克表明,如果感染有机体的转移速度快于受感染个体的恢复速度,那么疾病就会蔓延。”
他说:“如果情况相反,这种疾病将会灭绝。”“虽然Kermack和McKendrick证明了这一论断,但他们无法提供一个精确的,封闭的形式,基本微分方程的解析解,支配着各种种群的时间发展。”
从那以后,没有人能够找到一个不需要几页纸就能写出的方程的精确解。
贝尔德博士说:“我和我的合著者道格·巴洛(Doug Barlow)在寻找精确解决方案方面与我们的前辈没有什么不同。”“然而,我们确实找到了退而求其次的东西,这是一个可以写在一行上的近似解析解。”
今年5月,贝尔德博士在亚特兰大举行的东南理论化学协会(Southeastern Theoretical Chemistry Association)会议上展示了这个模型。
贝尔德博士说:“世界卫生组织可以将我们的方程式编程到掌上电脑中。”“我们的公式能够预测受感染人数达到最大值所需的时间。在化学模拟中,这被称为诱导时间。”
这个公式可以预测住院人数,死亡率、社区暴露率及相关变量。它还计算了易感人群、传染性人群和康复人群的数量,并预测了疾病起病期和消退期之间的清晰分离
贝尔德博士说:“在发病期间,感染人数稳步增加,因此康复人数的增长速度也会加快。”“为了减缓传播,缓解效应需要将注意力集中在一个被称为r - 0的参数上。”
r - 0是扩散速率除以恢复速率。
Baird博士说:“如果r - 0的值大于单位,疾病就在传播。”“如果r - 0的值小于单位,这种疾病就会灭绝。”
为了达到灭绝阶段公共卫生官员想要降低传播的速度,同时提高恢复的速度。Baird博士说:“疾病的消退期开始于感染者人数达到最大值之后。”
在下沉期间,受感染的个体数量开始减少,而恢复的个体数量仍在增加,但速度正在放缓。
贝尔德博士说:“在我们的结果中,还有一个公式,当与发病期间收集的人口数据相结合时,可以用来预测需要住院治疗的感染者人数预计达到最大值的时间。”
他说:“为了了解我们公式的准确性,我们将其预测结果与我们使用MathCad计算机软件生成的kermark - mckendrick方程的数值解进行了比较。”“在所有尝试过的情况下,我们的解析解和计算机解之间的差异从来没有超过2%。”
贝尔德博士的好奇心是在2020年被描述COVID-19感染人数迅速增加的新闻报道激发的。
他说:“感染率最初会加速,直到达到一个点,即感染率与感染者的康复率相平衡,在这个点上,感染者的数量达到峰值,然后开始下降。”
这种机制使他想起了支配自催化反应的机制。
Baird博士说:“后来我了解到,传染病传播的数学描述是由Kermack和McKendrick首先描述的。”
“当我读他们的论文时,我意识到他们的机理与自催化反应完全相同,即一个催化剂分子与一个反应物分子结合,产生两个催化剂分子,”他说。“催化剂分子的生成速度会加快,直到它与形成产物的催化剂的衰变速度相平衡。”
这项研究发表在国际化学动力学杂志.
进一步探索